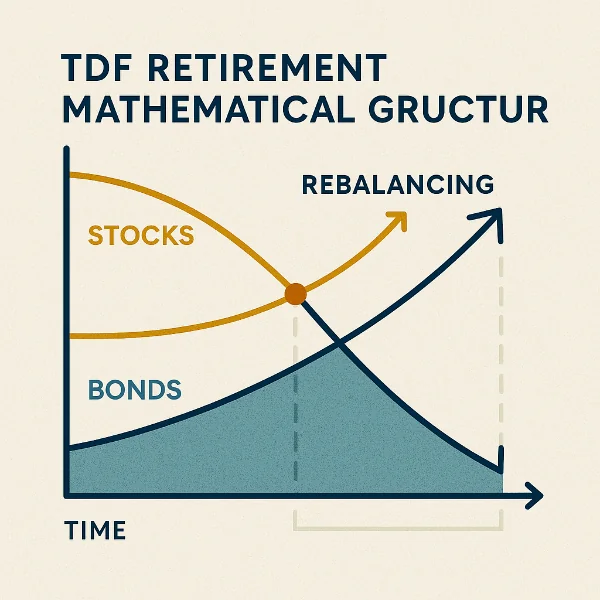
타깃데이트펀드(TDF)는 퇴직연금 가입자의 은퇴 시점을 기준으로 포트폴리오 위험을 자동 조정하는 상품이다. TDF의 리밸런싱 구조는 단순한 주식·채권 비중 조정이 아니라, 수학적 최적화(Optimization) 와 행태경제학적 투자행동 모델에 기반하여 설계된다. 본문에서는 TDF 리밸런싱의 수학적 공식, 민감도 분석, 기대효용 접근, 그리고 정책적 시사점을 학문적으로 분석한다.
목차
- TDF의 법적·제도적 구조
- 수학적 리밸런싱 모델과 공식
- 기대효용 최적화 접근
- 변수 민감도 분석 및 투자 효과
- 행태경제학적 투자행동과 정책 설계
- 결론: 지속가능한 TDF 설계 방향
TDF의 법적·제도적 구조
법적 근거:
- 「근로자퇴직급여 보장법」
주요 요건:
- 타깃 연도(Target Date): 은퇴 시점 기준
- 초기 위험자산 비중: 일반적으로 80% 이하
- 은퇴 시점 위험자산 비중: 20~40%
관리 주체:
- 금융기관 및 자산운용사
규제:
- 리밸런싱 전략 공시 의무
수학적 리밸런싱 모델과 공식
Glide Path 함수:
w_s(t) = w_0 × e^(-λt)
- w_s(t): 시점 t의 위험자산 비중
- w_0: 초기 위험자산 비중
- λ: 위험감소 속도계수
- t: 경과 시간(년)
리밸런싱 조건:
w_s(t) + w_b(t) = 1
- w_b(t): 안전자산 비중
최적화 목표:
Max E[U(W_T)]
- W_T: 은퇴 시점의 포트폴리오 가치
- U: 기대효용 함수
포트폴리오 가치:
W_T = Σ [w_s(t) × R_s + w_b(t) × R_b]
- R_s, R_b: 위험자산 및 안전자산의 기대수익률
기대효용 최적화 접근
효용 함수:
U(W) = (W)^(1 - ρ) / (1 - ρ), ρ > 0
- ρ: 상대적 위험회피 계수
최적 Glide Path 조건:
∂U/∂w_s(t) = λ × E(R_s - R_b) - γ × σ²
- γ: 위험회피 가중치
- σ²: 포트폴리오 분산
정책적 의미:
- 시간 경과에 따라 위험자산 비중을 감소시키면서 기대효용을 극대화
변수 민감도 분석 및 투자 효과
민감도 분석:
∂w_s/∂X, X ∈ {λ, R_s, R_b, ρ}
| 변수 변화 | 위험자산 비중 변화 |
| λ +0.01 | 위험자산 비중 연평균 -2%p |
| R_s - R_b +1%p | 위험자산 비중 +3%p |
| ρ(위험회피) +0.5 | 위험자산 비중 -1.5%p |
Monte Carlo 시뮬레이션:
- 시장수익률(R_s, R_b)와 λ의 확률분포 설정 → 포트폴리오 가치(W_T) 기대값과 분산 추정
E(W_T) = Σ (p_i × W_T,i)
Var(W_T) = Σ (p_i × (W_T,i - E(W_T))²)
행태경제학적 투자행동과 정책 설계
현재편향(Present Bias):
- 투자자가 장기적 위험조정 필요성을 과소평가
프레이밍 효과:
- Glide Path 설명 방식에 따라 투자자의 위험 선호도 변화
디폴트 옵션(Default Option) 효과:
- TDF 자동가입 시 투자참여율 증가
정책적 대응:
- 자동가입 권장
- 투자 위험 설명 방식 표준화
결론: 지속가능한 TDF 설계 방향
TDF의 수학적 리밸런싱 구조는 시간에 따른 위험감소를 최적화하면서 기대효용을 극대화하는 설계다. 변수 민감도 분석과 Monte Carlo 시뮬레이션은 투자자의 다양한 위험 선호를 반영하고, 행태경제학적 설계는 투자자의 장기적 참여를 촉진한다. 향후 TDF 정책은 표준화된 Glide Path와 디폴트 옵션 강화를 중심으로 발전할 필요가 있다.
FAQ
Q1. Glide Path는 왜 중요한가요?
시간 경과에 따른 위험조정 전략으로, 투자자 보호와 수익 최적화의 핵심이다.
Q2. 위험자산 비중은 어떻게 결정되나요?
시장 수익률, 투자자의 위험회피 성향, 나이 등을 반영해 수학적으로 최적화된다.
Q3. 민감도 분석이 중요한 이유는?
시장 변수 변화에 따른 포트폴리오 조정 필요성을 이해하는 데 도움된다.
Q4. 기대효용 이론은 어떻게 적용되나요?
투자자의 위험 선호에 따라 최적 포트폴리오 비중을 설정하는 데 사용된다.
Q5. 행태경제학이 왜 설계에 포함되나요?
투자자의 심리적·행동적 편향을 고려해 참여율과 지속성을 높일 수 있다.
관련글 제안
'정책·재정·금융 설계분석' 카테고리의 다른 글
| 금리상승기 채권형 펀드 손익구조: 듀레이션과 볼라틸리티의 함수 (2) | 2025.05.24 |
|---|---|
| 주택청약 가점제의 통계적 공정성 분석과 정책적 한계 (0) | 2025.05.23 |
| 청년형 ISA 설계 분석: 조세 이연과 기대효용 이론 (2) | 2025.05.21 |
| 기초연금 소득인정액 산정방식의 오류 가능성: 통계적 소득 포착 문제 (0) | 2025.05.20 |
| 실업급여 지급 기준의 통계학적 설계: 도덕적 해이와 최적화 모델 (1) | 2025.05.19 |